Przykład 1
W okrąg wpisano trójkąt w taki sposób, że jego najdłuższy bok zawierał się w średnicy tego okręgu. Wiemy, że jego dwa krótsze boki wynosiły: x+1 oraz x+2. Oblicz najmniejszą wartość trzeciego z boków i oceń, czy trójkąt o wyliczonych bokach może istnieć.

Oznaczmy długość trzeciego boku jako y. Z warunku budowy trójkąta wiemy, że najdłuższy z nich musi być krótszy niż suma długość dwóch pozostałych a ponadto każdy z boków musi być większy od 0. Zapiszmy ten warunek:



Podsumowanie: 
Sporządźmy rysunek opisujący sytuację zachodzącą w tym przykładzie:

Wiemy, że jedynym trójkątem którego jeden z boków jest średnicą okręgu na nim opisanego jest trójkąt prostokątny (np. z twierdzenia sinusów). Teraz w łatwy sposób obliczymy wartość y korzystając z twierdzenia Pitagorasa:




Oznaczmy funkcję podpierwiastkową jako h(x) = . Pierwiastek jest funkcją rosnącą zatem jej wartość minimalna jest taka sama jak wartość minimalna funkcji h(x). Obliczmy ją:
h’(x) =
0 =

Wyliczyliśmy, że najmniejsza wartość trzeciego boku wynosi  dla , ale wiemy jednocześnie, że .
Wniosek: Trójkąt prostokątny o przyprostokątnych x+1 i x+2 oraz minimalnej przeciwprostokątnej nie istnieje.

Przykład 2
Dla jakich wartości parametru m,  wyrażenie , gdzie  to różne pierwiastki funkcji kwadratowej opisanej wzorem f(x), jest najmniejsze?

Aby istniały dwa różne pierwiastki funkcji kwadratowej, musi zachodzić:


Korzystając z wzorów Viete’a obliczmy wartość wyrażenia :
 
Niech h(x)Liczymy pochodną h’(x):

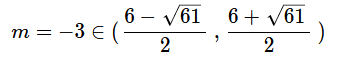
UWAGA: Nie liczymy wartości funkcji w krańcach dziedziny, gdyż  to jedyne ekstremum tej funkcji (ponadto wiemy że jest ono minimum a nie maksimum ze względu na znak pochodnej).

Wniosek: Parametr m jest równy -3.

Przykład 3
Ciąg (aₙ) jest ciągiem arytmetycznym, w którym  a wyrażenie  jest możliwie jak najmniejsze. Wyznacz

Ze wzoru na ciąg arytmetyczny otrzymujemy:

 
Wiemy, że wierzchołkiem funkcji kwadratowej jest  (możemy oczywiście skorzystać z pochodnej lub z równości ). Liczymy resztę ciągu arytmetycznego:


Możemy już bezpośrednio wyliczyć ,  korzystając z równości :

Zadania do zrobienia

1. Suma długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka jest równa 54 cm  . Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Jakie są długości krawędzi tego prostopadłościanu, który ma największą objętość?

Odp. .

2. Wydajność pracy pewnego robotnika zmienia się w ciągu ośmiogodzinnego dnia pracy i po  godzinach od jej rozpoczęcia osiąga wartość , gdzie . O której godzinie wydajność robotnika jest największa, jeśli rozpoczyna on pracę o godz. ?

Odp.  o godzinie