Dane są dwa zbiory: , . Ze zbioru A losujemy jedną cyfrę po czym losujemy ponownie jedną cyfrę ze zbioru B i z wylosowanych cyfr tworzymy liczbę dwucyfrową. Przedstawmy opisaną sytuację graficznie:

Widzimy, że w przypadku naszego doświadczenia mamy sześć różnych wyników:
Ω
Co więcej drzewko stochastyczne umożliwia obliczanie prawdopodobieństw poszczególnych zdarzeń. Oczywiście w rozważanym przez nas zdarzeniu wybór każdej z cyfr jest jednakowo prawdopodobny:

A więc mamy:

Przykład 1

Strzelec trafia do tarczy z prawdopodobieństwem równym 0,75. Oblicz prawdopodobieństwo zdarzenia w którym strzelec oddając trzy strzały trafia za pierwszym lub dopiero za trzecim razem.

Niech T oznacza, że strzelec trafił w cel a N, że strzelec chybił. Literką A oznaczmy interesujące nas wydarzenie losowe (A – strzelec oddaje trzy strzały i trafia za pierwszym lub za trzecim razem) Sporządźmy drzewko przedstawiające tą sytuację:

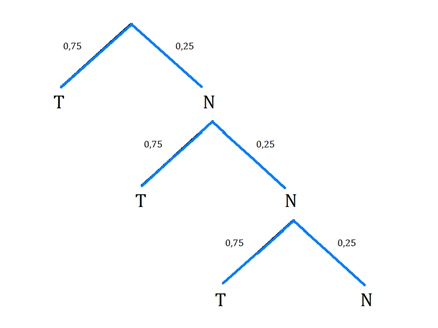
Ω


Prawdopodobieństwo trafienia za pierwszym lub trzecim razem jest równe

Zadania do zrobienia

1. W rzucie niesymetryczną monetą  prawdopodobieństwo otrzymania orła jest równe , a reszki - . Oblicz prawdopodobieństwo otrzymania dwóch orłów w trzykrotnym rzucie ta monetą.

Odp. .

2.  Strzelec trafia do tarczy z prawdopodobieństwem  0,7. Ma 4 naboje. Postanowił strzelać do pierwszego trafienia lub do wyczerpania nabojów. Oblicz prawdopodobieństwo zdarzenia, że strzelec trafi do tarczy.

Odp. 0,9919.

3. Rzucamy siedem razy symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia:

a) co najmniej raz wypadła reszka

b) reszka wypadła co najwyżej jeden raz.

Odp. a)

         b) .