Przykład 1

Wyznacz na paraboli o postaci  taki punkt, że jego odległość od punktu  jest najmniejsza. Podaj tę odległość.

Interesujący nas punkt oznaczmy literką P. Oznaczmy współrzędne tego punktu jako , wówczas  

Wiemy, że kwadrat liczby rzeczywistej jest nieujemny, zatem aby  było minimalne parametr  musi być równy zeru. (UWAGA: Do policzenia minimum mogliśmy skorzystać z rachunku pochodnych, co jest niewątpliwie najbardziej uniwersalną metodą rozwiązywania zadań tego typu) Ostatecznie otrzymujemy że szukany punkt ma współrzędne  a szukana odległość wynosi .

Przykład 2

Znajdź taki prostokąt, że jego dwa wierzchołki należą do paraboli o równaniu  a dwa pozostałe należą do prostej  a jego pole jest największe możliwe. Oblicz to pole.

Zauważmy najpierw że prostokąt jest figurą symetryczną (jeśli „przetniemy go na pół” to otrzymamy z dwóch stron taką samą figurę). Analogiczna sytuacja zachodzi dla paraboli o równaniu . Wiemy że osią symetrii dowolnej paraboli  jest , a więc mamy że każdy z punktów należących do szukanego prostokąta leży w symetrii do punktu . Jesteśmy więc w stanie stwierdzić że punkty leżące „na lewo” od osi symetrii mają współrzędne , a te leżące „na prawo”: . Jeśli  to wartość paraboli w tym punkcie wynosi  (Zwróć uwagę że jeśli  to , a więc rzędne zgadzają się). Ostatecznie:

Musimy założyć, że , gdyż tylko wtedy prostokąt o największym polu może istnieć.

Rozważmy funkcję :

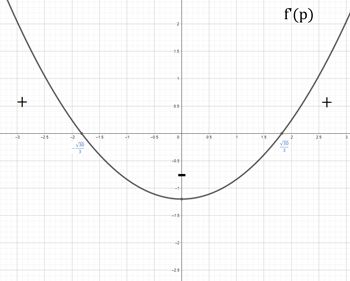
Obie wartości spełniają założenie więc:

Wskażmy pole tego największego prostokąta i jego wierzchołki:

Zadania do zrobienia