
Układy równań pierwszego stopnia z dwiema niewiadomymi.
Definicja 1: Układem dwóch równań pierwszego stopnia z
dwiema niewiadomymi x i y nazywamy koniunkcję takich równań i oznaczamy:
{a2x+b2y=c2
Gdzie a12+b12>0 i a22+b22>0
Jeżeli mamy układ dwóch równań, które mają postać wzoru funkcji liniowej, to rozwiązać go znaczy po prostu znalezienie punktu wspólnego wykresów obu funkcji, w przypadku równania pierwszego stopnia takie rozwiązanie może być jedno, czyli wykresy przecinają się w wspólnym punkcie, nieskończenie wiele, czyli wykresy nachodzą na siebie, lub mogą nie mieć rozwiązania, czyli wykresy nigdy się nie spotykają.
Na powyższym wykresie dwie proste przecinają się w jednym punkcie, współrzędne tego punktu (x, y) są jedynym rozwiązaniem układu równań. Jest to układ oznaczony
Na powyższym wykresie proste się pokrywają, czyli każda para liczb spełniające jedno z równań, spełnia też drugie, rozwiązań takiego układu jest nieskończenie wiele, jest to układ nieoznaczony.
Na powyższym wykresie proste są równoległe, nigdy się nie spotkają, więc taki układ nie będzie miał rozwiązania, taki układ jest sprzeczny.
Przykład 1
Mamy układ równań
, teraz staramy się obliczyć x lub y, w tym
przypadku najłatwiej będzie obliczyć y.
, teraz nasz obliczony y
podstawiamy do pierwszego równania.
, teraz możemy obliczyć nasz
x
, pozostaje nam obliczyć y
, w ten sposób obliczyliśmy
x i y.
Przykład 2
Mamy układ równań:
, teraz pomnóżmy równanie 2
razy 2
, otrzymamy wtedy:
, teraz dodajmy oba równania
stronami:
, możemy już bez problemu obliczyć x

Kolejnym sposobem może być rozwiązanie układu równań za pomocą wyznacznika macierzy:
, taki układ równań możemy
zapisać w prostokątnej tablicy zwanej macierzą.
, jednak w praktyce lepiej
posługiwać się macierzą kwadratową (na studiach ogarniesz czemu J), w tym przypadku
będzie to
wyglądało tak:
,
,
, z macierzy kwadratowej można obliczyć jej
wyznacznik.
(Pamiętaj że symbol macierzy różni się od symbolu wyznacznika macierzy.)
Przykład 3
Oblicz wyznacznik macierzy
Korzystając ze wzoru z definicji mamy:
5*3-(-5*2)=15-(-10)=15+10=25
Wróćmy do naszego układu równań:
, a12+b12>0 i a22+b22>0
Wprowadźmy teraz pewne oznaczenia:
W= Wx=
Wy=
Ma tylko jedno rozwiązanie, jeśli W≠0
Ma nieskończenie wiele rozwiązań, jeśli W=Wx=Wy=0
Nie ma rozwiązań, jeśli W=0 i (Wx≠0 lub Wy≠0)
Przykład 4
Rozwiąż układ równań:
Zaczynamy od obliczenia wyznaczników:
W=
Wx=
Wy=
W= 11*(-34) –((-22)*32)=-374+704=330
Wx=68*(-34)-(8*32)=-2312-256=-2568
Wy=11*8-((-22)*68)=88+1496=1584
x=
y=
Zadania do zrobienia
1. Rozwiąż układy równań metodą
podstawiania
Odp.
2. Rozwiąż układy równań metodą
przeciwnych współczynników
Odp. układ sprzeczny
3. Rozwiąż układy równań metodą graficzną
Odp.
4. Rozwiąż układy równań, stosując wyznaczniki
a)
b)
Odp. a)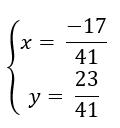
b)
5. Dopisz brakujące równanie układu tak, aby powstały układ równań:
a) był sprzeczny
b) był nieoznaczony
c) był oznaczony