Definicja: Funkcją homograficzną nazywamy funkcję wymierną y= , gdzie c≠0 i ad - cb≠0. Dziedziną funkcji homograficznej jest zbiór R- {}.

Przykład 1

Która funkcja jest funkcją homograficzną ? Wybierz tą funkcję i narysuj jej wykres:
f(x)=  

g(x)=

h(x)=

Funkcja f nie jest homograficzna, bo c=0, g także ponieważ ad-cb = 12-12=0. Jedyną funkcją homograficzną jest funkcja h (przykład c) ).
Wykres funkcji: Wykresem funkcji jest tzw. hiperbola.

Przykład 2

Narysuj wykres funkcji f(x)=

Przekształcamy wykres funkcji do postaci kanonicznej:  +q, gdzie p i q są asymptotami wykresu funkcji, kolejno: p – asymptota pionowa, q – asymptota pozioma.

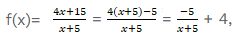
Asymptoty funkcji: x=-5, y=4, miejsce zerowe: x= =  , f(0)=3
Wykres funkcji: 

Zadania do zrobienia

1. Wśród poniższych funkcji znajdują się funkcje homograficzne. Wskaż je.

a) F(x) =

b) G(x) =

Odp.      a) jest b) nie jest

2. Wykres funkcji F(x) = , gdzie x  R - {2}, powstał w wyniku przesunięcia równoległego wykresu funkcji y =  o wektor  = [a, b]. Wyznacz współrzędne wektora .

Odp.  = [2, -1]

3. Wyznacz zbiór tych argumentów, dla których funkcja:

a) F(x) =  przyjmuje wartości nieujemne

b) G(x) =  przyjmuje wartości niedodatnie

Odp.      a) x  

               b) x  (-, -8)