W 1 klasie są omawiane funkcje trygonometryczne kąta skierowanego.
Przypomnijmy to zagadnienie:

Wtedy:
1) sinα =
2) cosα =
3)  tgα  =  , gdzie x≠0
4) ctgα =  , gdzie y≠0
Wiadomo że dziedziną funkcji sinus i cosinus są liczby rzeczywiste, a funkcji tangens liczby rzeczywiste z wyjątkiem π/2 +kπ , k. Wynika to z wykresów tych funkcji.

Podstawowe tożsamości trygonometryczne:

Przykład 1.

Wiedząc, że tgα = - i α, obliczymy sinα, cosα,  ctgα.

Wiadomo że ctgα = , zatem ctgα =-

Następnie obliczymy sinα oraz cosα:

Korzystając z własności 1) oraz 2), tworzymy układ równań i rozwiązujemy go:
 

12 sinα = -5 cosα /:12

 /144

169  = 144  /:169

  oraz  α, zatem cosα < 0

Odp. Szukane wartości to: , , ctgα = -  .

Przedstawmy wzory redukcyjne, umożliwią nam one rozwiązywanie równań jak i później nierówności trygonometrycznych. Są to wzory umożliwiające zapisanie większych na pierwszy rzut oka trudnych wartości funkcji trygonometrycznych za pomocą mniejszych argumentów o znanych nam wartościach.

Na co należy zwrócić uwagę korzystając z wzorów redukcyjnych?

Znane wartości kątowe. Zawsze próbujemy do nich sprowadzić wyrażenie.

Znak wyrażenia. Zależy on od ćwiartki w której znajduję się dana wartość.

Uwaga: Przydatna w zapamiętywaniu znaku funkcji trygonometrycznych jest rymowanka „w pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens a w czwartej cosinus.

3. Jeżeli we wzorze znajduje się nieparzysta wielokrotność   + α lub   , to funkcja zmienia się na kofunkcje. Oznacza to że sinus zmienia się na cosinus, a tangens zmienia się na cotangens. W innym wypadku funkcja pozostaje bez zmian.

Przykład 2.

Obliczymy wartość wyrażeń:
a)                                 b)

Rozwiązanie:

(Jest to IV ćwiartka, zatem cosα > 0)

1

(Jest to III ćwiartka, zatem tgα > 0 )

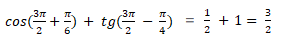
Ad b.

) = sin() = sin(π -   

) = ctg() = - 
2.   + 1

Okresowość funkcji trygonometrycznych

Przypomnijmy definicje funkcji okresowej:
Funkcje nazywamy okresową wtedy i tylko wtedy, gdy istnieje taka liczba T różna od zera, że dla każdej liczby x należącej do dziedziny funkcji f liczba x + T należy do dziedziny tej funkcji oraz zachodzi równość f(x + T) = f(x), gdzie T jest okresem funkcji f. Jeśli istnieje najmniejszy okres dodatni funkcji, nazywamy go okresem podstawowym(zasadniczym).

Okres podstawowym funkcji sinus oraz cosinus jest liczba 2π, zapisujemy to: T0= 2π , zatem

sin(2π +x ) = sinx  oraz  cos(2π + x) = cosx             , x

Okresem podstawowym funkcji tangens oraz cotangens jest π, zapisujemy to : T0= π , zatem

tg(π + x ) = tgx , x -

ctg(π + x ) = ctgx , x -

Przykład 3.

Obliczmy okres podstawowy funkcji:
f(x) = sin(5x)                      b)cos(

Rozwiązanie:

T0 – okres podstawowy funkcji f, zatem:

f(x + T0) = sin[5(x + T0)]= sin(5x + 5T0)

Funkcja f jest okresowa zatem zachodzi równość: f(x + T0) = f(x), otrzymujemy

sin(5x + 5T0) = sin5x,

wprowadzam zmienną α = 5x, więc sin(α +5T0) = sinα

Okresem podstawowym funkcji sinus jest 2π, zatem 5T0 = 2π, więc T0 =

Odp: Okresem podstawowym funkcji f(x) = sin(5x) jest liczba .

Parzystość i nieparzystość funkcji trygonometrycznych

Warunek parzystość funkcji: f(-x) = f(x)
Warunek nieparzystości funkcji: f(-x) = -f(x)
Jest to prawdziwe jeśli x oraz -x należą do tej samej dziedziny.
Warto zauważyć, że:
funkcja y = cos x jest funkcją parzystą, dla x ∈ R, ponieważ cos(x) = cos(-x)
pozostałe funkcje są funkcjami nieparzystymi.

Zbiór wartości funkcji trygonometrycznych

Zbiorem wartości funkcji;
sinus oraz cosinus jest przedział liczb <-1,1>
tangens oraz cotangens jest zbiór liczb rzeczywistych.

Przykład 4

Wyznaczmy zbiór wartości funkcji f(x) =

Wiadomo że,  -1≤ cos2x  ≤1 ,

Musimy przekształcić nierówność w sposób równoważy tak abyśmy pośrodku otrzymali naszą zadaną funkcje.

-1≤ cos2x  ≤1 /

-≤ cos2x  ≤/-3

--3 ≤ cos2x - 3  ≤- 3

Odp: Zbiorem wartości jest przedział liczbowy <--3, -3>.

Zadania do zrobienia