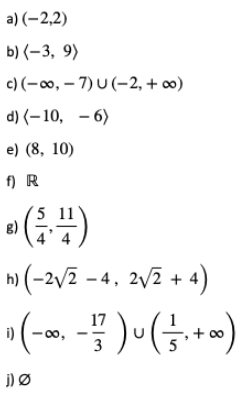1. Wartość bezwzględna

Definicja 

Wartość bezwzględną z liczby rzeczywistej x oznaczamy jako |x| i definiujemy jako:

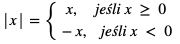
Uwaga: Dla dowolnej liczby rzeczywistej zachodzi:

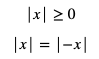
Przykład 1.

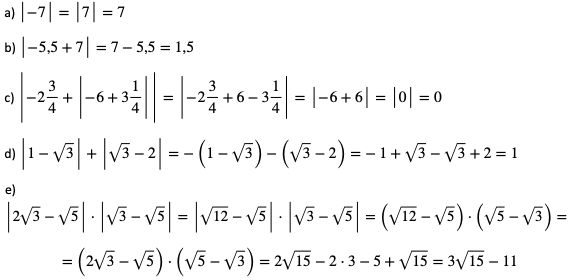
Twierdzenie Geometryczna interpretacja wartości bezwzględnej na osi liczbowej

Odległość na osi liczbowej między dwoma liczbami x i y wynosi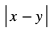

Uwaga: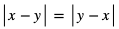  

Przykład 2.

a) Odległość na osi liczbowej między liczbami 27 i -18 wynosi:

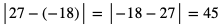
b) Odległość na osi liczbowej między liczbami 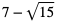 oraz 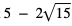 wynosi: 

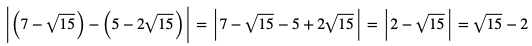
Zadania :

1. Oblicz wartości wyrażeń:

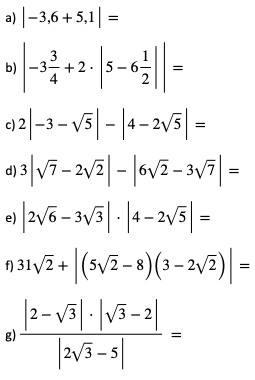
2. Wyznacz odległość na osi liczbowej pomiędzy liczbami:

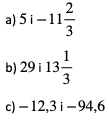
Odpowiedzi:

1)

a)  1.5 b) 0.75 c) 10 d) 0 e)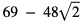   

f) 44  g)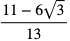   

2) 

a) 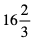 b) 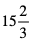 c)  82.3

2. Równania z wartością bezwzględną

Przykład. Rozwiąż równania:

a)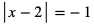  

Jest to równanie sprzeczne, ponieważ wartość bezwzględna nie może przyjmować wartości ujemnych. Stąd .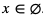

b)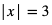  

Możliwe są dwa rozwiązania tego równania: x = 3  lub x = -3 

c)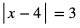  

Wyrażenie w wartości bezwzględnej może przyjmować wartość 3 lub -3. Stąd:

  x - 4 = 3 lub x - 4 = -3  

  x = 7 lub x = 1   są rozwiązaniami tego równania.

d)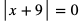  

Wartość bezwzględna przyjmuje wartość 0 wtedy i tylko wtedy, gdy wyrażenie pod wartością bezwzględną jest równe 0.

Stąd 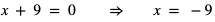  jest rozwiązaniem tego równania

e)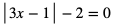  

Przekształcamy równanie do postaci: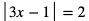  

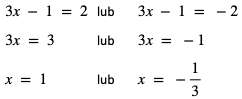
f)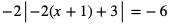  

Dzielimy najpierw obustronnie przez -2 otrzymując równanie: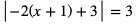  

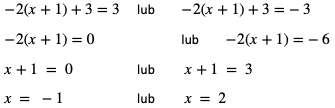
g)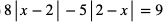  

Korzystamy z faktu, że 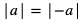dla dowolnej liczby rzeczywistej  a, zatem  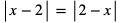i dostajemy równanie:

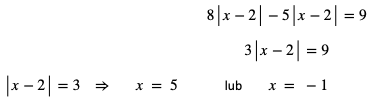
Zadanie:  Rozwiąż równania:

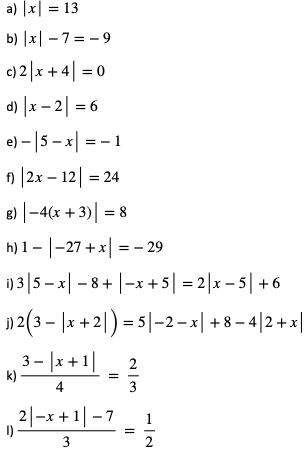
Odpowiedzi:

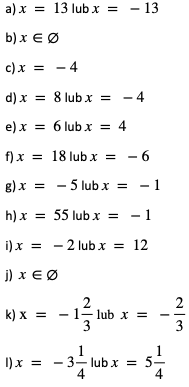
3. Nierówności z wartością bezwzględną

Przykład 1. Rozwiążemy nierówności :

a)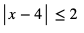  

Wyrażenie 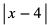oznacza odległość liczby x od liczby  4. Zatem szukamy takich  x, dla których odległość od 4 jest mniejsza lub równa  2. Możemy w tym celu posłużyć się osią liczbową. Zaznaczmy zbiór takich x, że odległość od x do 4 jest mniejsza lub równa 2.

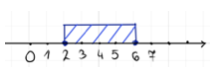
Zatem rozwiązaniem nierówności jest przedział:  <2; 6>

b)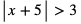  

Wyrażenie 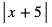możemy zapisać inaczej jako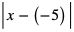. Oznacza ono zatem odległość liczby x od liczby -5. Szukamy takich x, dla których odległość od -5  jest większa niż 3  

Zatem rozwiązaniem nierówności  jest suma przedziałów: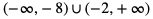  

Przykład 2. Rozwiążemy nierówności

a)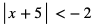  

Nierówność jest sprzeczna, bo wartość bezwzględna przyjmuje wartości jedynie nieujemne. Stąd rozwiązaniem jest zbiór pusty:  .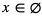

b)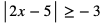  

Nierówność jest spełniona dla każdego 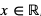 , bo lewa strona nierówności jest zawsze nieujemna.

c)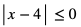  

Lewa strona nierówności jest zawsze nieujemna. Zatem nierówność ma rozwiązanie tylko wtedy, gdy 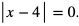  Stąd rozwiązaniem nierówności jest  x = 4.

d)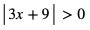  

Lewa strona nierówności jest zawsze nieujemna, zatem rozwiązaniem jest zbiór liczb rzeczywistych, z wyjątkiem tych  x, dla których 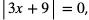  czyli z wyjątkiem  x = -3. 

e)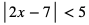  

Aby nierówność była spełniona, musi zachodzić równocześnie:

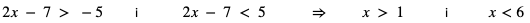
Czyli rozwiązaniem nierówności jest przedział (1,6).

f)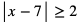  

Aby nierówność była spełniona, musi zachodzić równocześnie:

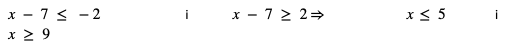
Czyli rozwiązaniem nierówności jest suma przedziałów :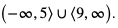 

Zadanie.  Rozwiąż nierówności:

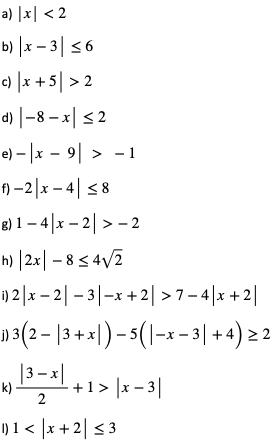
Odpowiedzi: