1. Potęga o wykładniku naturalnym

Definicja 1.

Potęgą o wykładniku naturalnym n, n > 0 i podstawie a, gdzie a jest dowolną liczbą rzeczywistą, nazywamy liczbę 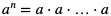, gdzie liczba a występuje w tym iloczynie n razy.

Przyjmujemy: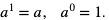 

Uwaga: 

• Wyrażenie 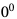nie ma określonej wartości liczbowej
• a2, czyli drugą potęgę liczby a nazywamy kwadratem liczby a
• a3, czyli trzecią potęgę liczby a nazywamy sześcianem liczby a

Przykład 1. Obliczmy potęgi wprost z definicji

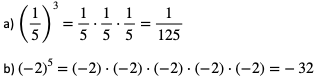
Twierdzenie 1. Własności potęg o wykładnikach naturalnych

Jeśli m, n – liczby naturalne i a, b – liczby rzeczywiste, to prawdziwe są własności:

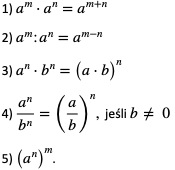
Przykład 2. Obliczmy korzystając z własności potęgowania

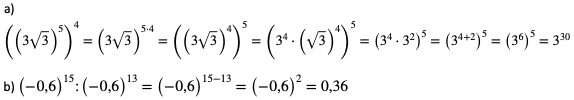
Przykład 3.

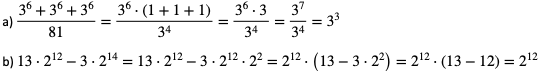
Przykład 4. Wykaż, że liczba 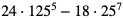jest podzielna przez 17.

Aby pokazać, że dana liczba jest podzielna przez 17, wystarczy zapisać ją w postaci iloczynu liczb naturalnych, którego jednym z czynników będzie liczba 17. Zamieńmy 125 i 25 na potęgi o podstawie 5:

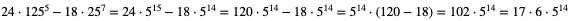
Zadanie 

1. Oblicz:

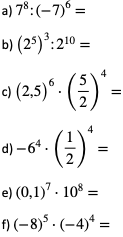
2. Oblicz:

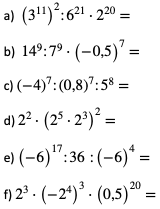
3. Oblicz:

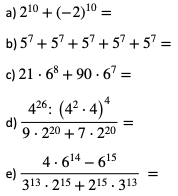
4. Udowodnij, że:

a) 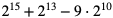jest podzielna przez 31

b) 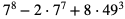jest podzielna przez 43 

Odpowiedzi:

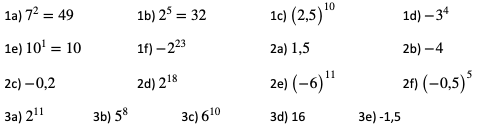
2. Pierwiastki

Definicja 1.

Pierwiastkiem stopnia n – tego, 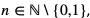 z nieujemnej liczby a nazywamy taką liczbę nieujemną b, dla której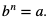 

Uwaga:

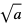• nazywamy pierwiastkiem kwadratowym z a
• 
  
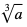• nazywamy pierwiastkiem sześciennym z a
• 
  
• Jeśli 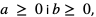 to symbolicznie możemy zapisać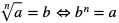
  
• 
  
• Jeśli dodatkowo n jest liczbą nieparzystą, to 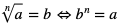zachodzi także dla a < 0

Twierdzenie 1. Własności pierwiastków

Jeśli 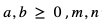 to liczby naturalne większe od 1, a p jest liczbą naturalną dodatnią, to:

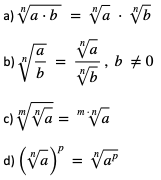
Jeśli dodatkowo n jest liczbą nieparzystą, to twierdzenie jest prawdziwe dla dowolnych a, b.

Przykład.  

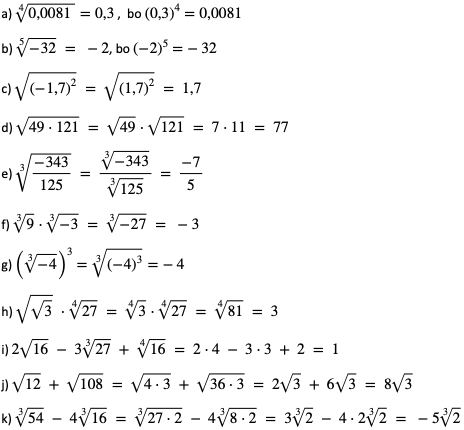
Zadanie Oblicz wartości wyrażeń:

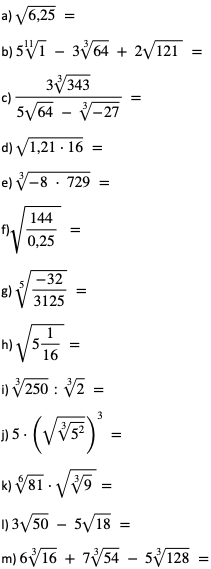
Odpowiedzi:

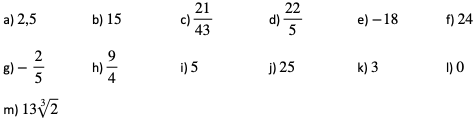
3. Potęga o wykładniku całkowitym ujemnym

Potęgę o wykładniku ujemnym zapisujemy jako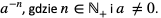    

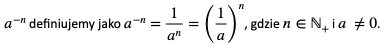
Uwaga: Zachodzą własności analogiczne jak dla potęg o wykładnikach naturalnych, to znaczy: 

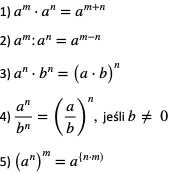
Przykład 1. 

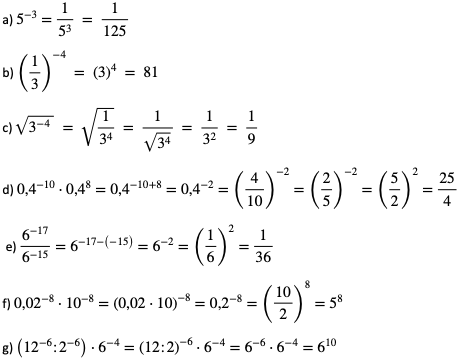
• Notacja wykładnicza
  
  

Każdą liczbę dodatnią x > 0 można przedstawić w postaci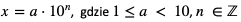    

Każdą liczbę ujemną x < 0  można przedstawić w postaci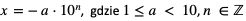    

Przykład 2. 

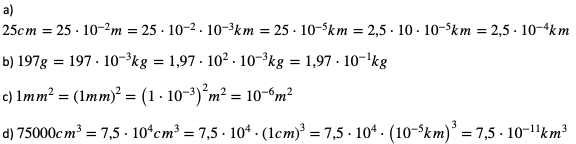
Zadania 

1. Oblicz:

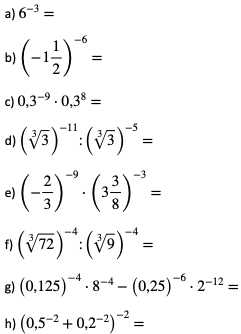
2. Zamień jednostki, wynik zapisz w postaci notacji wykładniczej.

Odpowiedzi:

4. Potęga o wykładniku wymiernym

Potęgę o wykładniku wymiernym 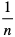definiujemy jako pierwiastek stopnia n:

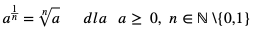
Przykład 1.

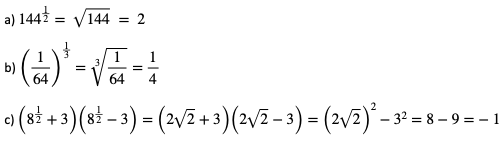
Potęgę o wykładniku wymiernym 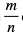definiujemy następująco:

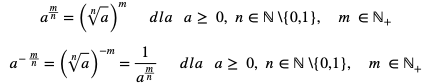
Uwaga: Dla dowolnych liczb wymiernych x i y, oraz dowolnych liczb rzeczywistych a, b, zachodzą własności analogiczne jak dla potęg o wykładnikach całkowitych: 

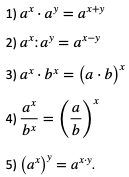
Przykład 2.

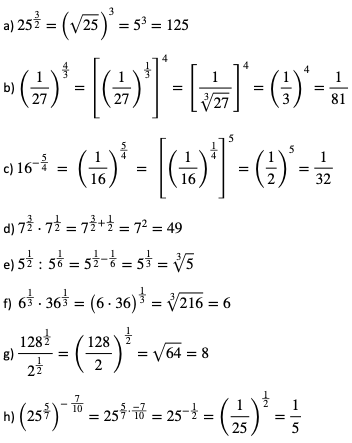
Zadania:  

1. Oblicz wartości wyrażeń:

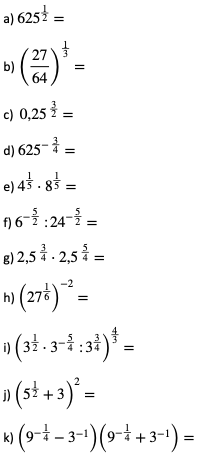
2. Zapisz w postaci jednej potęgi:

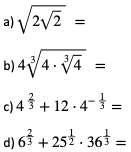
Odpowiedzi:

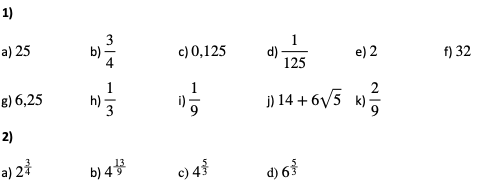
  b)   

5. Potęga o wykładniku rzeczywistym

• Można określić potęgę o dowolnej podstawie dodatniej i dowolnym wykładniku niewymiernym dodatnim. 
• Potęgi te mają te same własności co potęgi o wykładnikach wymiernych

Przykład

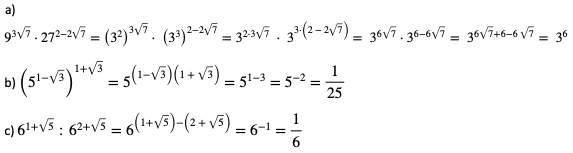
Zadanie:

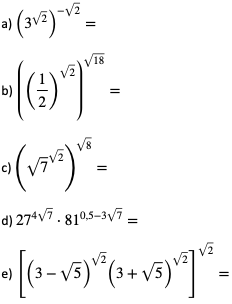
Odpowiedzi: