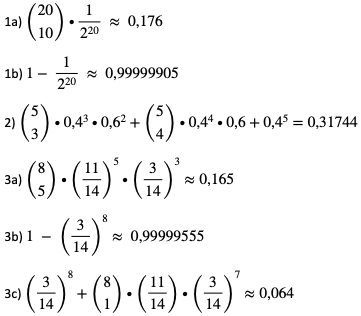Schemat Bernoulliego

Rozważamy doświadczenie losowe, które może skończyć się sukcesem lub porażką. Prawdopodobieństwo sukcesu oznaczamy literą p, a prawdopodobieństwo porażki literą q, gdzie q = 1 - p.  Pojedyncze doświadczenie spełniające te warunki nazywamy próbą Bernoulliego.

Przykład 1

1. Próbą Bernoulliego jest rzut symetryczną monetą. Za sukces możemy uznać wypadnięcie orła, a za porażkę wypadnięcie reszki. Wtedy
   
   
    .
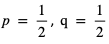2. Próba Bernoulliego może być rzut sześcienną kostką do gry. Za sukces możemy uznać wypadnięcie liczby oczek większej lub równej 5, a za porażkę liczbę oczek mniejszą niż 5. Wtedy
   
   
   . 

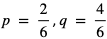Definicja 1

Schematem Bernoulliego nazywamy ciąg niezależnych powtórzeń tego samego doświadczenia losowego, które może zakończyć się jednym z dwóch możliwych wyników zwanych sukcesem lub porażką. Prawdopodobieństwo sukcesu i prawdopodobieństwo porażki w każdym powtórzeniu jest stałe.

Oznaczenia 

Prawdopodobieństwo uzyskania k sukcesów w schemacie n prób Bernoulliego dla 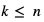będziemy oznaczać jako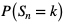 

Twierdzenie 1

W schemacie n prób Bernoulliego prawdopodobieństwo 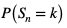otrzymania k sukcesów, gdzie 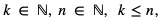wyraża się wzorem:

Przykład 2

Rzucamy 10 razy dwoma monetami. Oblicz prawdopodobieństwo zdarzenia  - orła na obu monetach otrzymamy: 

1. dokładnie 6 razy
2. co najmniej raz
3. co najwyżej trzy razy.

Nasze doświadczenie losowe jest schematem Bernoulliego o 10 próbach. W pojedynczej próbie Bernoulliego w tym doświadczeniu prawdopodobieństwo sukcesu – otrzymania orła na obu monetach,

 wynosi 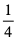. Prawdopodobieństwo porażki z kolei to  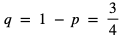( Oznaczmy wypadnięcie orła jako O, a wypadnięcie reszki jako R. Przestrzeń  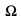składa się z czterech zdarzeń

 elementarnych: 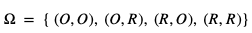 Sprzyjające jest tylko zdarzenie (O, O)).

1. Oznaczmy zdarzenie A – w 10 próbach otrzymano dokładnie 6 sukcesów

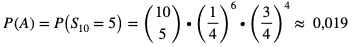
1. Oznaczmy zdarzenie B – w 10 próbach otrzymano co najmniej jeden sukces

W tym przypadku wygodnie jest posłużyć się prawdopodobieństwem przeciwnym. Zdarzenie przeciwne do B to B’ – w 10 próbach nie otrzymano żadnego sukcesu

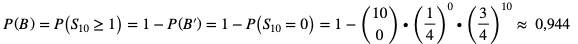
1. Oznaczmy zdarzenie C – w 10 próbach Bernoulliego otrzymamy sukces co najwyżej trzy razy.

Zdarzenie C można przedstawić w postaci sumy czterech parami wykluczających się zdarzeń 

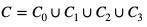
gdzie   to zdarzenie – w 10 próbach Bernoulliego otrzymano dokładnie i sukcesów dla i = 0, 1, 2, 3.

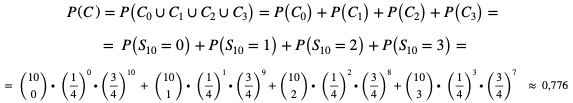
Zadania 

1. Rzucamy 20 razy sześcienną kostką do gry. Oblicz prawdopodobieństwo wypadnięcia liczby oczek będącej pierwszą: 
1. 10 razy
2. co najmniej jeden raz
2. Z działa oddano 5 strzałów do celu. Prawdopodobieństwo trafienia w cel w każdym strzale jest równe 0,4. Aby cel został uznany za zniszczony, powinien zostać trafiony co najmniej trzy razy. Oblicz prawdopodobieństwo zniszczenia celu. 
3. W urnie jest 6 kul białych i 10 czarnych. Z urny losujemy 3 kule, oglądamy je i z powrotem wrzucamy do urny. Doświadczenie to powtarzamy 8 razy. Oblicz prawdopodobieństwo zdarzenia:
1. 5 razy wylosowano co najmniej jedną kulę biała,
2. co najmniej raz wylosowano co najmniej jedną kulę białą,
3. co najwyżej raz wylosowano co najmniej jedną kulę białą. 

Odpowiedzi do zadań