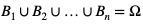Wzór Bayesa

Twierdzenie 1 Prawdopodobieństwo całkowite

Niech A będzie zdarzeniem zawartym w przestrzeni . Jeśli zdarzenia będą zdarzeniami zawartymi w tej samej przestrzeni  spełniającymi warunki:

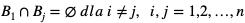1.  (czyli zdarzenia  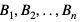wykluczają się parami)

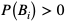1.   dla i = 1,2, ..., n  

to zachodzi wzór:

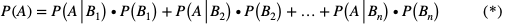
Wzór (*) nazywamy wzorem na prawdopodobieństwo całkowite.  

Twierdzenie 2 Wzór Bayesa 

Niech A będzie zdarzeniem zawartym w przestrzeni 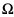. Jeśli zdarzenia 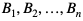będą zdarzeniami zawartymi w tej samej przestrzeni 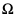, spełniającymi warunki:

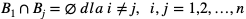1. (czyli zdarzenia  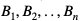wykluczają się parami)

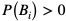1. dla i = 1,2, ..., n

to zachodzi wzór: 

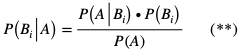
gdzie P(A) jest równe wzorowi (*) z Twierdzenia 1.

Wzór (**) nazywamy wzorem Bayesa.

Przykład 1

W pierwszym pudełku znajduje się 6 kul czarnych i 4 kule białe, a w drugim 8 kul czarnych i 7 kul białych. Rzucamy monetą. Jeśli wypadnie orzeł – losujemy jedną kulę z pierwszego pudełka. Jeśli wypadnie reszka – losujemy jedną kulę z drugiego pudełka. Wylosowana kula okazała się być czarna. Jakie jest prawdopodobieństwo, że pochodzi ona z pierwszego pudełka ?

Rozwiązanie :

a) Oznaczmy zdarzenia:

 A – wylosowano czarną kulę

 B1 – wylosowano kulę z pudełka pierwszego

 B2 – wylosowano kulę z pudełka drugiego

Szukamy prawdopodobieństwa 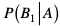. Korzystamy ze wzoru Bayesa:

Do obliczenia P(A) skorzystamy z twierdzenia i prawdopodobieństwie całkowitym:

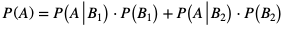
 Mamy 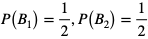, bo prawdopodobieństwo otrzymanie orła i reszki jest jednakowe. 

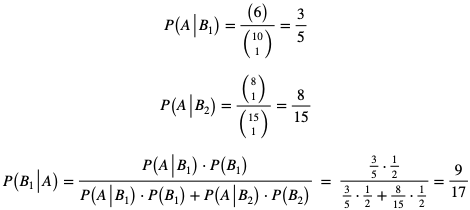
Zadania

1. W pierwszym pudełku znajduje się 5 kul niebieskich i 3 kule czerwone, a w drugim pudełku – 4 kule niebieskie i 1 kula czerwona. Rzucamy symetryczną sześcienną kostką do gry. Jeśli wypadną mniej niż trzy oczka, to losujemy jedną kulę z pierwszego pudełka. W przeciwnym przypadku losujemy jedną kulę z drugiego pudełka.

a) Oblicz prawdopodobieństwo wylosowania kuli czerwonej.

b) Wylosowana kula okazała się czerwona. Jakie jest prawdopodobieństwo, że kula pochodziła z pudełka drugiego.

2. Test wykrywający chorobę jest efektywny w 99 % dla osób chorych (tzn. jeśli badany jest chory, test w 99% przypadków potwierdza chorobę) i w 98 % dla osób zdrowych (tzn. jeśli badany jest zdrowy, test w 98% przypadków wyklucza chorobę. W pewnym regionie średnio 150 na 10 000 osób cierpi na tę chorobę.

a) Oblicz prawdopodobieństwo zdarzenia: test wykonany na losowo wybranej osobie z tego regionu wykluczy u niej chorobę

b) U losowo wybranej osoby z tego regionu test wykluczył chorobę. Oblicz prawdopodobieństwo zdarzenia: losowo wybrana osoba cierpi na tę chorobę.   

3. Fabryka samochodów osobowych wyprodukowała ten sam model samochodu w trzech kolorach: białym, czerwonym i zielonym. Stosunek liczby wyprodukowanych samochodów odpowiednio w tych kolorach był równy 6:9:5. Prawdopodobieństwo poprawnego położenia powłoki lakierniczej jest równe: dla samochodu białego 0,98, dla samochodu czerwonego 0,96 i dla samochodu zielonego 0,97. Spośród wyprodukowanych samochodów wybrano losowo jeden.

a) Oblicz prawdopodobieństwo zdarzenia: wybrany samochód jest wadliwie polakierowany i jest w kolorze białym.

b) Oblicz prawdopodobieństwo zdarzenia: wybrany samochód jest wadliwie polakierowany.

c) Okazało się, że wybrany samochód jest wadliwie polakierowany. Oblicz prawdopodobieństwo zdarzenia: wybrany samochód jest w kolorze zielonym.

Odpowiedzi