Zadania na dowodzenie z zastosowania średniej arytmetycznej, geometrycznej i kwadratowej

Definicja 1 

Średnia arytmetyczna liczb 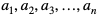jest równa  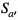gdzie 

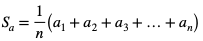
Definicja 2

 Średnia geometryczna liczb dodatnich 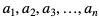jest równa  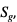gdzie 

Definicja 3

 Średnia kwadratową liczb 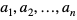jest równa  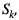gdzie 

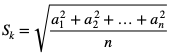
Jeśli liczby 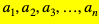  są dodatnie, to między średnimi  zachodzi następująca zależność: 

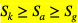
przy czym równość występuje tylko wtedy, gdy a1 = a2 = a3 = ... = an

Przykład 1 

Wykażemy, że dla dowolnej liczby dodatniej m, suma liczby m i jej odwrotności jest większa lub równa 2, czyli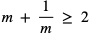  

Dowód: Z założenia m > 0, więc 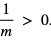 . Skorzystamy z nierówności między średnią arytmetyczną a średnią geometryczną dla liczb m i  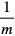. Mamy:

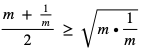
czyli 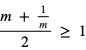 . A stąd  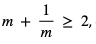co kończy dowód.

Przykład 2

Wykażemy, że jeśli a > 0, to zachodzi nierówność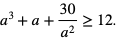 

Dowód:  Liczbę 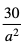przedstawiamy w postaci sumy  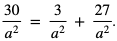Ponieważ a > 0, więc możemy skorzystać z nierówność między średnią arytmetyczną a średnią geometryczną:

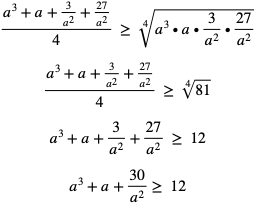
Przykład 3

Wykażemy, że jeśli liczby dodatnie a, b, c spełniają nierówność:  a + b + c > 7, to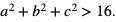  

Dowód: Ponieważ a + b + c > 7, to 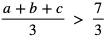 . Ponieważ liczby a, b, c są dodatnie to możemy skorzystać z nierówności między średnią kwadratową, a arytmetyczną:

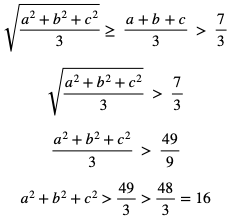
Zadania 

1.  Wykaż, że jeśli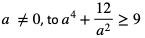   

2. Wykaż, że jeśli a, b, c, d są liczbami dodatnimi to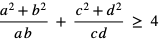  

3. Wykaż, że jeśli liczby a, b, c są dodatnie, to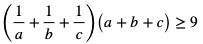 

4. Wykaż, że jeśli a > 0, to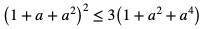 

5. Wykaż, że jeśli a, b, c są liczbami dodatnimi oraz 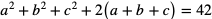, to 

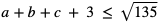
Wskazówki:

1. Zastosować nierówność między średnią arytmetyczną i geometryczną dla liczb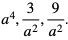 

2. 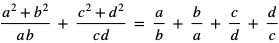 i nierówność między średnią arytmetyczną i geometryczną.

3. Zależność między średnią arytmetyczną i geometryczną liczb 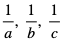i podobnie liczb a, b, c.

4. Zależność między średnią arytmetyczną i średnią kwadratową liczb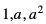

5. 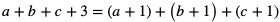 i nierówność między średnią arytmetyczną i średnią kwadratową liczb: a + 1, b + 1, c + 1.