Pochodna funkcji złożonej

Definicja 1

Niech będą dane dwie funkcje 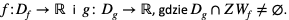 Niech 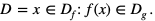 Wówczas funkcję, która

będziemy oznaczać 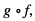określoną w zbiorze D następującym wzorem 

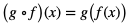
Nazywamy złożeniem funkcji f i g lub funkcją złożoną z funkcji f i g. Funkcję f będziemy nazywać funkcją wewnętrzną, natomiast g – funkcją zewnętrzną dla

funkcji złożonej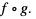 

Uwaga Operacja składania funkcji nie jest przemienna, tzn. 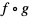 to nie to samo co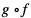

Przykład 1

Dane są funkcje 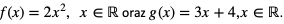. Wyznaczyć złożenie:

a)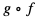 

Mamy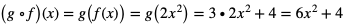 

Dziedziną funkcji f oraz funkcji g jest zbiór . Wszystkie wartości funkcji f należą do dziedziny funkcji g, więc dziedziną funkcji 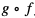jest zbiór .

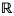b)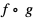 

Mamy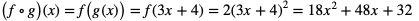 

Dla każdej liczby rzeczywistej z dziedziny funkcji g, wartości funkcji g należą do dziedziny funkcji f. Zatem dziedziną złożenia 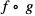 jest zbiór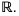 

Przykład 2

Dane są funkcje 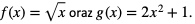Wyznaczyć złożenie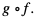 

Dziedziną funkcji f jest przedział 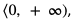 a dziedziną funkcji g jest zbiór 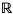. Dziedziną złożenia 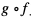jest zbiór tych wszystkich x z dziedziny funkcji f dla których f(x) należy do dziedziny

funkcji g. Zatem dziedziną złożenia 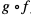jest przedział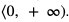 

Złożenie 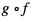wyraża się wzorem:

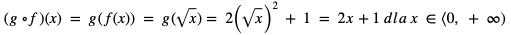
Twierdzenie 1 O pochodnej funkcji złożonej

Jeśli funkcja f ma pochodną w punkcie x, a funkcja g ma pochodną w punkcie f(x), to funkcja złożona 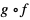ma pochodną w punkcie x i prawdziwa jest równość:

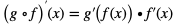
Uwaga  Twierdzenie 1 można podsumować tak: Pochodna funkcji złożonej równa się iloczynowi pochodnej funkcji zewnętrznej i pochodnej funkcji wewnętrznej.

Przykład 3

Wyznaczyć pochodne następujących funkcji:

a)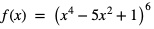  

Dziedziną funkcji f jest zbiór 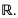 Funkcja f(x) jest funkcją złożoną, więc możemy przyjąć 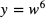za funkcję zewnętrzną, a 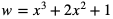za funkcję wewnętrzną. Obliczamy pochodną:

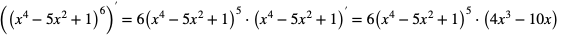
b)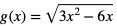 

Dziedziną funkcji g jest zbiór wszystkich x rzeczywistych spełniających warunek:

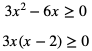
Stąd 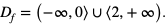 Za funkcję zewnętrzną przyjmujemy  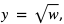a za funkcję wewnętrzną  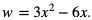Liczymy pochodną:

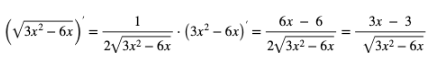
Twierdzenie 2 

Jeśli 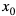jest n-krotnym pierwiastkiem wielomianu W(x) to 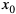jest (n-1) krotnym pierwiastkiem jego pochodnej, 

Przykład 4

Rozważmy wielomian 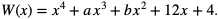 Wiadomo, że x = - 1 jest pierwiastkiem dwukrotnym tego wielomianu. Wyznaczyć a i b.

Na mocy twierdzenia 2. liczba -1 jest pierwiastkiem co najmniej dwukrotnym wielomianu W(x) jeśli spełnione będą warunki:

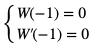
Wyznaczmy pochodną wielomianu: 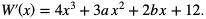 Dostajemy układ równań

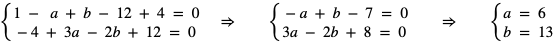
Dostajemy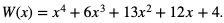 

Należy jeszcze uzasadnić, że dla wyznaczonych a i b liczba -1 nie jest pierwiastkiem trzykrotnym W(x).  Załóżmy nie wprost, że -1 jest pierwiastkiem trzykrotnym wielomianu. Wtedy z twierdzenia

wynika, że -1 jest pierwiastkiem dwukrotnym W(x),  gdzie 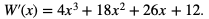 Sprawdźmy czy  

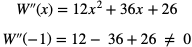
Otrzymaliśmy sprzeczność z założeniem, że liczba -1 jest pierwiastkiem trzykrotnym W(x).

Więc liczba -1 jest pierwiastkiem dwukrotnym W(x) dla a = 6, b = 13.

Zadania

1. Wyznaczyć złożenia 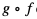 oraz 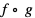i dziedziny tych złożeń:

2.  Wyznaczyć pochodną funkcji f i podać dziedzinę pochodnej.

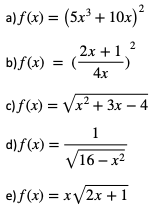
3. Wiadomo, że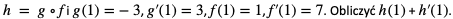    

4. Funkcje f i g są różniczkowalne w zbiorze oraz 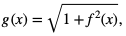. Wiedząc, że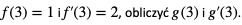      

Odpowiedzi