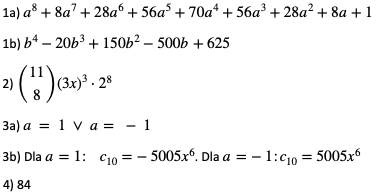Symbol Newtona, wzór Newtona, trójkąt Pascala

Definicja 1

Symbolem Newtona nazywamy symbol 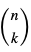określający liczbę podzbiorów k-elementowych zbioru n-elementowego.

Twierdzenie 1. Własności symbolu Newtona:

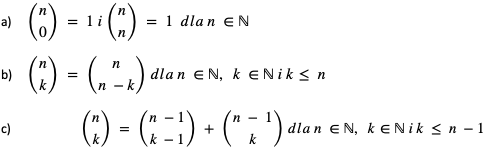
Twierdzenie 2. 

Dla dowolnej liczby naturalnej 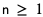 zachodzi wzór:

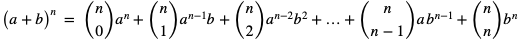
Definicja 2.

Wzór z twierdzenia 2 nazywamy dwumianem Newtona (wzorem Newtona).

Wypiszmy teraz kolejno współczynniki rozwinięcia dwumianu Newtona, gdzie 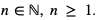 W pierwszym wierszu

wpisujemy 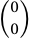, czyli 1. W kolejnych wierszach mamy:

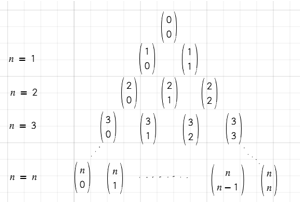
Definicja 3. Tablicę otrzymaną powyżej nazywamy trójkątem Pascala.

Własności trójkąta Pascala:

1. Współczynniki rozwinięcia, które są jednakowo odległe od początku i od końca wiersza są sobie równe. Wynika to ze wzoru 
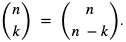
2. Każdy współczynnik rozwinięcia – oprócz jedynek na brzegach- jest sumą dwóch współczynników w trójkącie Pascala znajdujących się bezpośrednio nad nim.
   
   
   Wynika to ze wzoru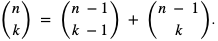  

Przykład 1 

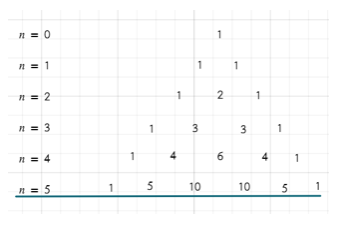
Obliczymy 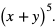 Kolejne współczynniki rozwinięcia bierzemy z trójkąta Pascala z wiersza dla n = 5. 

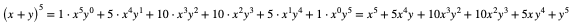
Przykład 2 

Suma symboli Newtona drugiego i czwartego wyrazu rozwinięcia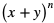 jest równa 64. Wyznacz szósty wyraz tego rozwinięcia.

Z warunków zadania mamy, że 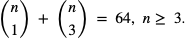 Mamy zatem:

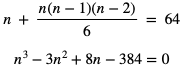
Można pokazać, że jedynym rozwiązaniem tego równania jest n = 8.

Szósty wyraz rozwinięcia 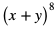jest postaci:

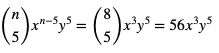
Zadania 

1. Zapisać w postaci sumy:

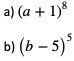
2. Wyznaczyć dziewiąty wyraz rozwinięcia .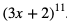

3. Współczynnik przy 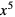wielomianu 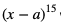w postaci uporządkowanej jest równy 3003. 

a) Obliczyć a

b) Dla wyznaczonej wartości a podać dziesiąty wyraz rozwinięcia dwumianu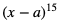 

4. Wyznaczyć wyraz rozwinięcia 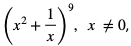 który nie zawiera x.

Odpowiedzi: