Bryła sztywna (dynamika ruchu obrotowego)
Zadanie 1: Do
krawędzi stołu przymocowany jest blok nieruchomy, będący jednorodnym krążkiem o
masie m3, obracającym się bez tarcia. Przez blok przełożona jest
bardzo lekka i nierozciągliwa linka, której jeden koniec doczepiony jest do
skrzynki o masie m1, a drugi do skrzynki o masie m2.
Pierwsza skrzynka leży na stole, a druga wisi na lince. Współczynnik tarcia
pierwszej skrzynki o stół oznaczamy jako ![]() (bez rozróżnienia współczynników tarcia
statycznego i kinetycznego). Moment bezwładności jednorodnego krążka (lub
walca) względem jego osi wyraża się wzorem
(bez rozróżnienia współczynników tarcia
statycznego i kinetycznego). Moment bezwładności jednorodnego krążka (lub
walca) względem jego osi wyraża się wzorem 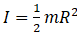 , gdzie R jest
promieniem krążka, a m – jego masą. W chwili początkowej obie skrzynki były
nieruchome. Wykaż, że podczas ruchu skrzynek ich przyspieszenie można wyrazić
wzorem
, gdzie R jest
promieniem krążka, a m – jego masą. W chwili początkowej obie skrzynki były
nieruchome. Wykaż, że podczas ruchu skrzynek ich przyspieszenie można wyrazić
wzorem
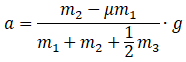
Skorzystaj ze wzorów wyrażających II
zasadę dynamiki dla bloku, pierwszej i drugiej skrzynki.
Zadanie 2: W górę równi pochyłej o kącie nachylenia α wtacza się bez poślizgu kula, która u podstawy równi ma szybkość v0. Oblicz drogę jaką przebędzie wzdłuż równi kula do chwili zatrzymania się.
Zadanie 3: Krążek o momencie bezwładności 0,01 kg∙m2 obracał się bez tarcia wokół swojej osi z prędkością kątową 32 rad/s. Na ten krążek spadł ciężarek o masie 0,6kg upuszczony bez prędkości początkowej. Ciężarek był połączony z osią krążka nitką ślizgającą się po osi bez tarcia. Po chwili ciężarek zaczął obracać się razem z krążkiem pozostając w odległości 10cm od osi obrotu. Rozmiary ciężarka można pominąć.
Napisz nazwę zasady zachowania, która pozwala wyznaczyć wspólną prędkość kątową krążka i ciężarka. Oblicz wartość tej prędkości kątowej.