
5 najczęściej popełnianych błędów na maturze rozszerzonej z matematyki
Zadania pojawiające się na maturze
podstawowej z matematyki potrafi być podchwytliwe. Jednak jak wtedy nazwać to
co czeka Cię na maturze rozszerzonej? W tym opisie przygotowałem 5 według mnie
najczęściej popełnianych błędów na maturze rozszerzonej z matematyki. Takich
przykładów można by oczywiście podać więcej, co ma miejsce na moich kursach
maturalnych. Pod koniec opisu można
znaleźć film z rozwiązaniem tych pięciu problemów.
Pierwszy błąd dotyczy skracania
stronami wyrażeń których wartość może wynosić zero. To karygodny i chyba
najczęściej popełniany błąd obliczeniowy na maturze zarówno podstawowej jak i
rozszerzonej. A dowodem na to było np. zadanie nr 13 na maturze maj 2015 poziom
rozszerzony. Nie wolno wyrażeń skracać stronami (takich które mogą wynosić
zero). Jeśli to zrobisz to po pierwsze gubisz rozwiązania, a po drugie dzielisz
przez zero. Za opuszczenie rozwiązań ukaże Cię egzaminator odjęciem odpowiedniej
ilości punktów. Pamiętaj cholero nie dzieli się przez zero!

Drugi błąd dotyczy źle
sformułowanych wzorów Viete’a na iloczyn. Na przykład dwa miejsce zerowe mają
być większe od 3. Czyli napiszesz że ich iloczyn jest większy od 9. I napiszesz
źle! To prawda, że ich iloczyn jest większy od 9. Jednak przypominam, że masz napisać
takie wzory Viete’a, z których będzie wynikały warunki zadania. Czy z tego że
iloczyn jest większy od 9 wynika, ze pierwiastki są większe od 3? Nie! Przykładem
są liczby 2 i 5. Ich iloczyn jest większy od 9, a one poszczególne nie są większe od 3. Warunek z iloczynem należy
robić zawsze w odniesieniu do zera czyli: (x1-3)(x2=3) > 0. Oto analogiczny
przykład pozywany na filmie:
Kolejny błąd dotyczy źle
podawanej cechy w dowodzeniu podobieństwa. W przypadku gdy punkty łączą środki
boków trójkąta nie wiemy, że powstały odcinek jest równoległy do jego podstawy
(jest to prawda, ale należałoby to udowodnić). Zatem nie możemy skorzystać z
cechy podobieństwa kąt- kąt- kąt (kkk). Ale możemy użyć cechy bok- kąt- bok,
ponieważ mamy pewność co do proporcjonalności boków i jednego kąta wspólnego. 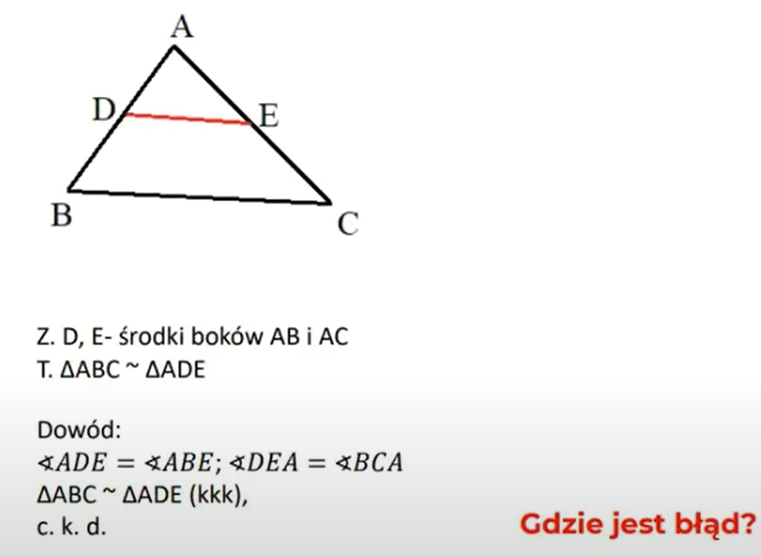
Kolejny błąd dotyczy rozwiązywania równań z pierwiastkiem. Takie równania są rozwiązywane poprzez podnoszenie stron do kwadratu. Uczniowie bardzo często pamiętają o założeniu, że wyrażenie znajdujące się pod pierwiastkiem jest nieujemne. Ale zapominają założyć, że druga strona równania- która jest równa pierwiastkowi- też musi być nieujemna. W końcu jest przyrównana do pierwiastka, który w swej naturze jest nieujemny. Zatem w przeciwnym przypadku dla pewnych argumentów mielibyśmy sprzeczność (np. 3 = -3), która po podniesieniu do kwadratu dałaby równanie poprawne (9 = 9). Idealnie odzwierciedla do poniższy przykład w którym rozwiązanie -16 zostało pomimo, że wykonując sprawdzenie dostajemy dla niego równanie sprzeczne (9 = -9).
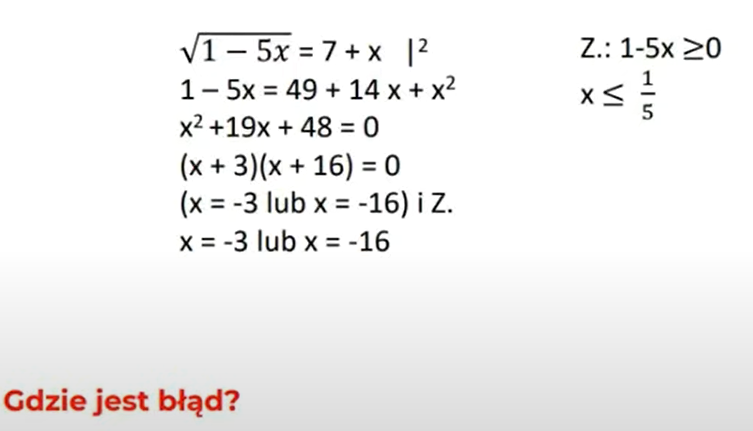
Ostatni wskazany przeze mnie błąd
na maturze dotyczy zagadnienia rachunku różniczkowego. Często uczniowie
analizując poglądowy rysunek pochodnej nie uwzględniają dziedziny, która ma
kluczowy wpływ na wnioski podejmowane z tego rysunku. Na przykład w poniższym
przykładzie obliczono ekstrema przyrównując pierwszą pochodną do zera i badając
czy pochodna zmieniła znak. Z tej analizy wynika, że funkcja powinna mieć dla
ekstrema. Ale jedno z nich nie należy do dziedziny funkcji zatem należy go
usunąć z rozwiązań.



