
Szczegółowe wymagania maturalne z matematyki na maturze 2025,2026 itd.
Wielu uczniów szkół średnich poświęca naprawdę sporo czasu,
żeby przygotować się
odpowiednio do egzaminu maturalnego, kiedy nadejdzie już właściwa pora. Żeby
jednak zrobić to rzetelnie, należałoby zacząć od zgłębienia wiedzy, jakie w
ogóle zagadnienia będą obowiązywały na maturze. Wymagania maturalne różnią się
bowiem na przestrzeni lat, warto zatem szanować swój jakże cenny czas i
przygotować się jak najlepiej z zagadnień, które możemy spotkać na egzaminie
maturalnym z matematyki na poziomie podstawowym czy też
rozszerzonym.
Poniżej znajdziesz spis wymagań szczegółowych obowiązujących od matury w formule 2025. Kolorem żółtym zaznaczone zostały zagadnienie, które w formule 2023 i 2024 wymagane były na poziomie rozszerzonym, a zostały przeniesione do poziomu podstawowego. Kolorem zielonym natomiast zagadnienia całkowicie nowe, których nie znajdziemy w wymaganiach z matur 2023 i 2024.
Wymagania szczegółowe CKE z zakresu podstawowego
I. Liczby rzeczywiste.
Uczeń:
1) wykonuje działania (dodawanie,
odejmowanie, mnożenie, dzielenie, potęgowanie, pierwiastkowanie,
logarytmowanie) w zbiorze liczb rzeczywistych;
2) przeprowadza proste dowody dotyczące podzielności liczb
całkowitych i reszt z dzielenia nie trudniejsze
niż:
a) dowód
podzielności przez 24 iloczynu czterech kolejnych liczb naturalnych,
b) dowód własności: jeśli liczba przy dzieleniu przez 4 daje resztę 3, to nie jest kwadratem liczby całkowitej;
3) stosuje własności pierwiastków
dowolnego stopnia, w tym pierwiastków stopnia nieparzystego z liczb ujemnych;
4) stosuje związek pierwiastkowania z potęgowaniem oraz prawa działań na potęgach i pierwiastkach;
5) stosuje własności monotoniczności potęgowania,
6) posługuje się pojęciem
przedziału liczbowego, zaznacza przedziały na osi liczbowej;
7) stosuje interpretację
geometryczną i algebraiczną wartości bezwzględnej, rozwiązuje równania i nierówności;
8) wykorzystuje własności potęgowania i pierwiastkowania w sytuacjach praktycznych, w tym do obliczania procentów składanych, zysków z lokat (względem matury 2024 odeszło natomiast obliczanie kosztów kredytów);
9) stosuje związek logarytmowania
z potęgowaniem, posługuje się wzorami na logarytm iloczynu, logarytm ilorazu i
logarytm potęgi.
II. Wyrażenia algebraiczne.
Uczeń:
1) stosuje wzory skróconego
mnożenia 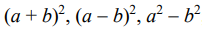 ;
;
2) dodaje, odejmuje i mnoży wielomiany jednej i wielu zmiennych;
3) wyłącza poza nawias jednomian
z sumy algebraicznej;
4) mnoży i dzieli wyrażenia
wymierne;
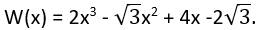 Ponadto nie znajduje się w niej również dodawanie i odejmowanie wyrażeń wymiernych, w przypadkach nie trudniejszych niż:
Ponadto nie znajduje się w niej również dodawanie i odejmowanie wyrażeń wymiernych, w przypadkach nie trudniejszych niż: 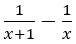 .
.
III. Równania i nierówności.
Uczeń:
1) przekształca równania i
nierówności w sposób równoważny;
2) interpretuje równania i
nierówności sprzeczne oraz tożsamościowe;
3) rozwiązuje nierówności liniowe
z jedną niewiadomą;
4) rozwiązuje równania i nierówności kwadratowe;
Względem matury 2024 zostało usunięte rozwiązywanie nierówności typu: Ix-2I < 3 oraz rozwiązywanie równań wielomianowych, które dają się doprowadzić do postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub metodą grupowania, a także rozwiązywanie równań wymierne postaci V(x)/W(x) = 0, gdzie wielomiany V(x) i W(x) są zapisane w postaci iloczynowej.
IV. Układy równań.
Uczeń:
1) rozwiązuje układy równań
liniowych z dwiema niewiadomymi, podaje interpretację geometryczną układów
oznaczonych, nieoznaczonych i sprzecznych;
2) stosuje układy równań do rozwiązywania zadań tekstowych;
V. Funkcje
Uczeń:
1) określa funkcje jako
jednoznaczne przyporządkowanie za pomocą opisu słownego, tabeli, wykresu, wzoru
(także różnymi wzorami na różnych przedziałach);
2) oblicza wartość funkcji
zadanej wzorem algebraicznym;
3) odczytuje i interpretuje
wartości funkcji określonych za pomocą tabel, wykresów, wzorów itp., również w
sytuacjach wielokrotnego użycia tego samego źródła informacji lub kilku źródeł
jednocześnie;
4) odczytuje z wykresu funkcji:
dziedzinę, zbiór wartości, miejsca zerowe, przedziały monotoniczności,
przedziały, w których funkcja przyjmuje wartości większe (nie mniejsze) lub
mniejsze (nie większe) od danej liczby, największe
i najmniejsze wartości funkcji (o ile istnieją) w danym przedziale domkniętym
oraz argumenty, dla których wartości największe i najmniejsze są przez funkcję
przyjmowane;
5) interpretuje współczynniki występujące we
wzorze funkcji liniowej;
6) wyznacza wzór funkcji liniowej
na podstawie informacji o jej wykresie lub o jej własnościach;
7) szkicuje wykres funkcji
kwadratowej zadanej wzorem;
8) interpretuje współczynniki
występujące we wzorze funkcji kwadratowej w postaci ogólnej, kanonicznej i
iloczynowej (jeśli istnieje);
9) wyznacza wzór funkcji
kwadratowej na podstawie informacji o tej funkcji lub o jej wykresie;
10) wyznacza największą i
najmniejszą wartość funkcji kwadratowej w przedziale domkniętym;
11) wykorzystuje własności
funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych,
fizycznych itp., także osadzonych w kontekście praktycznym;
12) na podstawie wykresu funkcji y = f(x) szkicuje wykresy funkcji y = f(x-a),
y = f(x) + b;
13) posługuje się funkcją f(x) = a/x, w tym jej wykresem, do opisu i interpretacji
zagadnień związanych z wielkościami odwrotnie proporcjonalnymi, również w
zastosowaniach praktycznych;
14) posługuje się funkcjami wykładniczą i logarytmiczną, w tym ich wykresami, do opisu i interpretacji zagadnień związanych z zastosowaniami praktycznymi.
W maturze 2025 nie znajdziemy już jednak zadań związanych ze szkicowaniem funkcji y = - f(x), y = f (-x) na podstawie wykresu y=f(x),
VI. Ciągi.
Uczeń:
1) oblicza wyrazy ciągu
określonego wzorem ogólnym;
2) oblicza początkowe wyrazy ciągów określonych rekurencyjnie;
3) w prostych przypadkach bada,
czy ciąg jest rosnący, czy malejący;
4) sprawdza, czy dany ciąg jest
arytmetyczny lub geometryczny;
5) stosuje wzór na n-ty wyraz i
na sumę n początkowych wyrazów ciągu arytmetycznego;
6) stosuje wzór na n-ty wyraz i
na sumę n początkowych wyrazów ciągu geometrycznego;
7) wykorzystuje własności ciągów,
w tym arytmetycznych i geometrycznych, do rozwiązywania zadań, również
osadzonych w kontekście praktycznym.
VII. Trygonometria.
Uczeń:
1) wykorzystuje definicje
funkcji: sinus, cosinus i tangens dla kątów od 0° do 180° , w szczególności
wyznacza wartości funkcji trygonometrycznych dla kątów 30°, 45°, 60°;
2) korzysta z wzorów na jedynkę trygonometryczną oraz tg;
3) stosuje twierdzenia cosinusów oraz wzór na pole trójkąta z wykorzystaniem sinusa
4) oblicza kąty trójkąta i długości jego boków przy odpowiednich
danych (rozwiązuje trójkąty prostokątne, w tym z wykorzystaniem funkcji trygonometrycznych).
VIII. Planimetria.
Uczeń:
1) wyznacza promienie i średnice
okręgów, długości cięciw okręgów oraz odcinków stycznych, w tym z wykorzystaniem twierdzenia Pitagorasa;
2) rozpoznaje trójkąty
ostrokątne, prostokątne i rozwartokątne przy danych długościach boków (m.in.
stosuje twierdzenie odwrotne do twierdzenia Pitagorasa i twierdzenie
cosinusów); stosuje twierdzenie: w trójkącie naprzeciw większego kąta
wewnętrznego leży dłuższy bok;
3) rozpoznaje wielokąty foremne i
korzysta z ich podstawowych własności;
4) korzysta z własności kątów i
przekątnych w prostokątach, równoległobokach, rombach i trapezach;
5) stosuje własności kątów
wpisanych i środkowych;
6) stosuje wzory na pole wycinka
koła i długość łuku okręgu;
7) stosuje twierdzenia: Talesa;
8) korzysta z cech podobieństwa
trójkątów;
9) wykorzystuje zależności między obwodami oraz między polami figur podobnych;
10) wskazuje podstawowe punkty szczególne w trójkącie: środek okręgu wpisanego w trójkąt, środek okręgu opisanego na trójkącie, ortocentrum, środek ciężkości oraz korzysta z ich własności;
11)stosuje funkcje
trygonometryczne do wyznaczania długości odcinków w figurach płaskich oraz
obliczania pól figur;
12) przeprowadza dowody geometryczne.
W przyszłorocznej maturze nie znajdziemy jednak zadań, w których należałoby wykorzystać twierdzenia o dwusiecznej kąta oraz o kącie między styczną a cięciwą.
IX. Geometria analityczna na
płaszczyźnie kartezjańskiej.
Uczeń:
1) rozpoznaje wzajemne położenie
prostych na płaszczyźnie na podstawie ich równań, w tym znajduje wspólny punkt
dwóch prostych, jeśli taki istnieje;
2) posługuje się równaniami prostych na płaszczyźnie, w
postaci kierunkowej i ogólnej, w tym wyznacza równanie prostej o zadanych
własnościach (takich jak na przykład przechodzenie przez dwa dane punkty, znany
współczynnik kierunkowy, równoległość do innej prostej);
3) oblicza odległość dwóch
punktów w układzie współrzędnych;
4) posługuje się równaniem okręgu
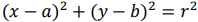 ;
;
5) wyznacza obrazy okręgów i
wielokątów w symetriach osiowych względem osi układu współrzędnych, symetrii
środkowej (o środku w początku układu współrzędnych).
Uczeń nie będzie musiał już jednak na poziomie podstawowym obliczać odległości punktu od prostej.
X. Stereometria.
Uczeń:
1) rozpoznaje wzajemne położenie
prostych w przestrzeni, w szczególności proste prostopadłe nieprzecinające się;
2) posługuje się pojęciem kąta między prostą a płaszczyzną oraz pojęciem kąta dwuściennego między półpłaszczyznami;
3) rozpoznaje w graniastosłupach i ostrosłupach kąty
między odcinkami (np. krawędziami, krawędziami i przekątnymi) oraz kąty między
ścianami, oblicza miary tych kątów;
4) rozpoznaje w walcach i w stożkach kąt między odcinkami
oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między
tworzącą a podstawą), oblicza miary tych kątów;
5) oblicza objętości i pola
powierzchni graniastosłupów, ostrosłupów, walca, stożka i kuli, również z wykorzystaniem trygonometrii;
6) wykorzystuje zależność między
objętościami brył podobnych.
XI. Kombinatoryka.
Uczeń:
1) zlicza obiekty w prostych
sytuacjach kombinatorycznych;
2) zlicza obiekty, stosując
reguły mnożenia i dodawania (także łącznie) dla dowolnej liczby czynności w sytuacjach nie trudniejszych niż:
a) obliczenie,
ile jest czterocyfrowych nieparzystych liczb całkowitych dodatnich takich, że w ich zapisie
dziesiętnym występuje dokładnie jedna cyfra 1 i dokładnie jedna cyfra 2,
b) obliczenie,
ile jest czterocyfrowych parzystych liczb całkowitych dodatnich takich, że w ich zapisie
dziesiętnym występuje dokładnie jedna cyfra 0 i dokładnie jedna cyfra 1.
XII. Rachunek
prawdopodobieństwa i statystyka.
Uczeń:
1) oblicza prawdopodobieństwo w
modelu klasycznym;
2) oblicza średnią arytmetyczną i
średnią ważoną, znajduje medianę i dominantę;
Z przyszłorocznej podstawy zniknął jednak wymóg obliczania odchylenia standardowego zestawu danych (także w przypadku danych odpowiednio pogrupowanych) oraz interpretacja tego parametru dla danych empirycznych;
XIII. Optymalizacja i rachunek
różniczkowy
Uczeń rozwiązuje zadania
optymalizacyjne w sytuacjach dających się opisać funkcją kwadratową.
Wymagania szczegółowe CKE z zakresu rozszerzonego
I. Liczby rzeczywiste
1) stosuje wzór na zamianę podstawy logarytmu;
II. Wyrażenia algebraiczne
1) dzieli wielomian jednej zmiennej W(x) przez dwumian postaci x - a;
2) rozkłada wielomiany na czynniki metodą wyłączania wspólnego czynnika przed nawias oraz metodą grupowania wyrazów;
3) znajduje pierwiastki całkowite wielomianu o współczynnikach całkowitych;
4) stosuje podstawowe własności trójkąta Pascala oraz
następujące własności współczynnika dwumianowego (symbolu Newtona) 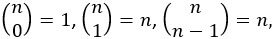
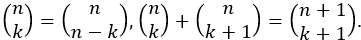 ;
;
5) korzysta ze wzorów na sumę dwóch wyrazów podniesionych do potęgi trzeciej, na sumę bądź różnicę dwóch wyrazów podniesioną do n-tej potęgi;
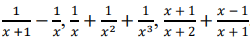 .
.
III. Równania i nierówności
1) rozwiązuje nierówności
wielomianowe dla
wielomianów doprowadzonych do postaci iloczynowej lub takich, które dają się
doprowadzić do
postaci iloczynowej metodą wyłączania wspólnego czynnika przed nawias lub
metodą grupowania;
2) rozwiązuje równania i nierówności wymierne, które dadzą się sprowadzić do równania lub nierówności liniowej lub kwadratowej;
3) stosuje wzory Viète’a dla
równań kwadratowych;
4) rozwiązuje równania i
nierówności z wartością bezwzględną;
5) analizuje równania i nierówności liniowe z parametrami oraz równania i nierówności kwadratowe z parametrami, w szczególności wyznacza liczbę rozwiązań w zależności od parametrów, podaje warunki, przy których rozwiązania mają żądaną własność, i wyznacza rozwiązania w zależności od parametrów;
6) rozwiązuje równania wielomianowe, które dają się doprowadzić do równania kwadratowego, w szczególności równania dwukwadratowe;
7) rozwiązuje równania wymierne postaci V(x)/W(x) = 0, gdzie wielomiany V(x) i W(x) są zapisane w postaci iloczynowej.
IV. Układy równań
1) rozwiązuje układy
równań liniowych i kwadratowych z dwiema niewiadomymi, które można sprowadzić do równania kwadratowego lub liniowego, a które nie są trudniejsze niż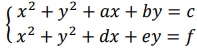
V. Funkcje
1) na podstawie wykresu funkcji y = f(x) rysuje wykresy funkcji y = -f(x), y = f(-x)
2) posługuje się złożeniami funkcji;
3) dowodzi monotoniczności funkcji zadanej wzorem 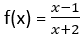 jest monotoniczna w przedziale
jest monotoniczna w przedziale ;
;
Z podstawy usunięto natomiast rysowanie
VI. Ciągi
1) oblicza granice ciągów,
korzystając z granic ciągów typu oraz twierdzeń o granicach sumy, różnicy,
iloczynu i ilorazu ciągów zbieżnych, a także twierdzenia o trzech ciągach;
2) rozpoznaje zbieżne szeregi
geometryczne i oblicza ich sumę.
VII. Trygonometria
1) stosuje miarę łukową, zamienia stopnie na radiany i odwrotnie;
2) posługuje się wykresami
funkcji trygonometrycznych: sinus, cosinus, tangens;
3) wykorzystuje okresowość
funkcji trygonometrycznych;
4) stosuje wzory redukcyjne dla
funkcji trygonometrycznych;
5) korzysta z wzorów na sinus, cosinus i tangens sumy i różnicy kątów, a także na funkcje trygonometryczne kątów podwojonych;
6) rozwiązuje równania i nierówności trygonometryczne;
7) stosuje twierdzenie sinusów;
8) oblicza kąty trójkąta i długości jego boków przy odpowiednich danych (rozwiązuje trójkąty).
VIII. Planimetria
1) stosuje własności czworokątów wpisanych w okrąg i opisanych na okręgu;
2) stosuje twierdzenie odwrotne do twierdzenia Talesa.
IX. Geometria analityczna na
płaszczyźnie kartezjańskiej
1) znajduje punkty wspólne prostej i okręgu;
2) znajduje punkty wspólne dwóch okręgów;
3) zna pojęcie wektora i oblicza jego współrzędne oraz długość, dodaje wektory i mnoży wektor przez liczbę, oba te działania wykonuje zarówno analitycznie, jak i geometrycznie;
4) wyznacza równanie prostej prostopadłej do zadanej prostej i prostej stycznej do zadanego okręgu.
X. Stereometria
1) zna i stosuje twierdzenie o
prostej prostopadłej do płaszczyzny i o trzech prostopadłych;
2) wyznacza przekroje sześcianu i
ostrosłupów prawidłowych oraz oblicza ich pola, także z
wykorzystaniem trygonometrii.
XI. Kombinatoryka
1) oblicza liczbę możliwych
sytuacji, spełniających określone kryteria, z wykorzystaniem reguły mnożenia i
dodawania (także łącznie) oraz wzorów liczbę: permutacji, kombinacji i
wariacji;
2) stosuje współczynnik
dwumianowy (symbol Newtona) i jego własności przy rozwiązywaniu problemów
kombinatorycznych.
XII. Rachunek
prawdopodobieństwa i statystyka
1) oblicza prawdopodobieństwo
warunkowe i stosuje wzór Bayesa, stosuje twierdzenie o prawdopodobieństwie całkowitym;
2) stosuje schemat Bernoullego.
XIII. Optymalizacja i rachunek
różniczkowy
1) oblicza granice funkcji (w tym
jednostronne);
2) stosuje własność Darboux do uzasadniania istnienia
miejsca zerowego funkcji;
3) stosuje definicję pochodnej funkcji, podaje interpretację geometryczną i fizyczną pochodnej;
4) oblicza pochodną funkcji potęgowej o wykładniku rzeczywistym oraz oblicza pochodną, korzystając z twierdzeń o pochodnej sumy, różnicy, iloczynu, ilorazu i funkcji złożonej;
5) stosuje pochodną do badania
monotoniczności funkcji;
6) rozwiązuje zadania
optymalizacyjne z zastosowaniem pochodnej.
Opis arkuszy egzaminacyjnych
1)
Poziom podstawowy
Na napisanie egzaminu maturalnego
na poziomie podstawowym przewidziane jest 180 minut. Arkusz będzie się składać
z od 29 do 40 zadań, natomiast całkowita możliwa do zdobycia liczba punktów
będzie wynosić 50 punktów.
|
RODZAJ ZADAŃ |
LICZBA ZADAŃ |
LICZBA PUNKTÓW |
UDZIAŁ W WYNIKU SUMARYCZNYM |
|
Zamknięte |
20-25 |
25 |
50% |
|
Otwarte |
9-15 |
25 |
50% |
|
RAZEM |
29-40 |
50 |
100% |
W arkuszu będzie znaleźć można
zadania pojedyncze albo powiązane tematem, przy czym każde z zadań
powiązanych będzie się dało rozwiązać niezależnie od wyniku z zadania
poprzedniego.
2)
Poziom rozszerzony
Czas przewidziany na napisanie
matury z matematyki na poziomie rozszerzonym wynosić będzie również 180 minut.
Łącznie będzie można w nim znaleźć od 10 do 14 zadań otwartych. W tym arkuszu
także będą zadania pojedyncze lub powiązane o wspólnym kontekście tematycznym.
Przykładowe zadania
W informatorach maturalnych
znaleźć można informację, iż zarówno dla egzaminu z 2023, jak i 2024 roku,
usunięto część zadań przewidzianych w podstawie programowej. Natomiast znaleźć
je już będzie można na egzaminie dojrzałości w roku 2025 czy 2026, a to kilka
przykładów:
1) Poziom podstawowy
2) Poziom rozszerzony
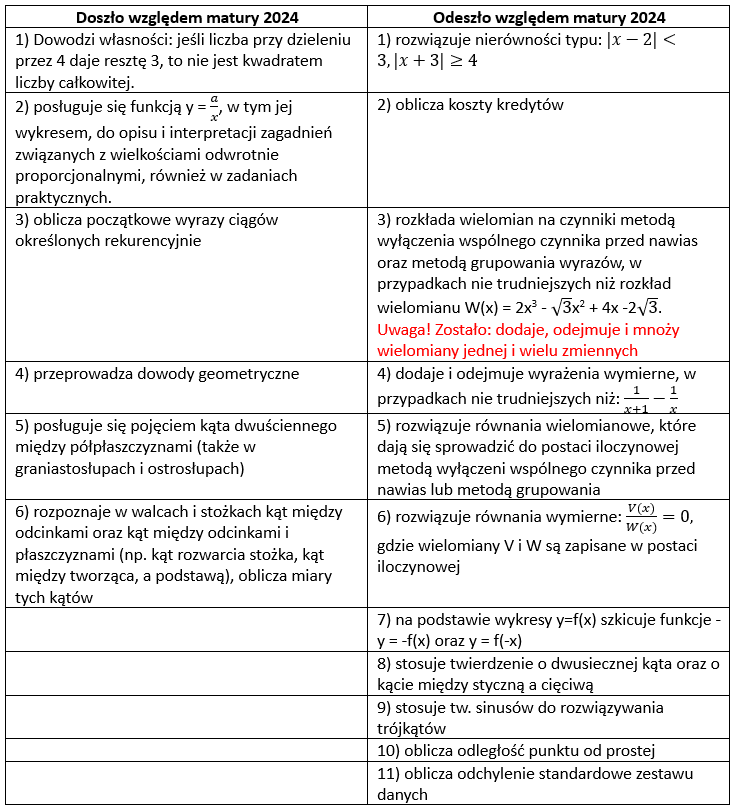
Zmiany względem podstawy programowej matury 2024 dla poziomu podstawowego przedstawia poniższa grafika:
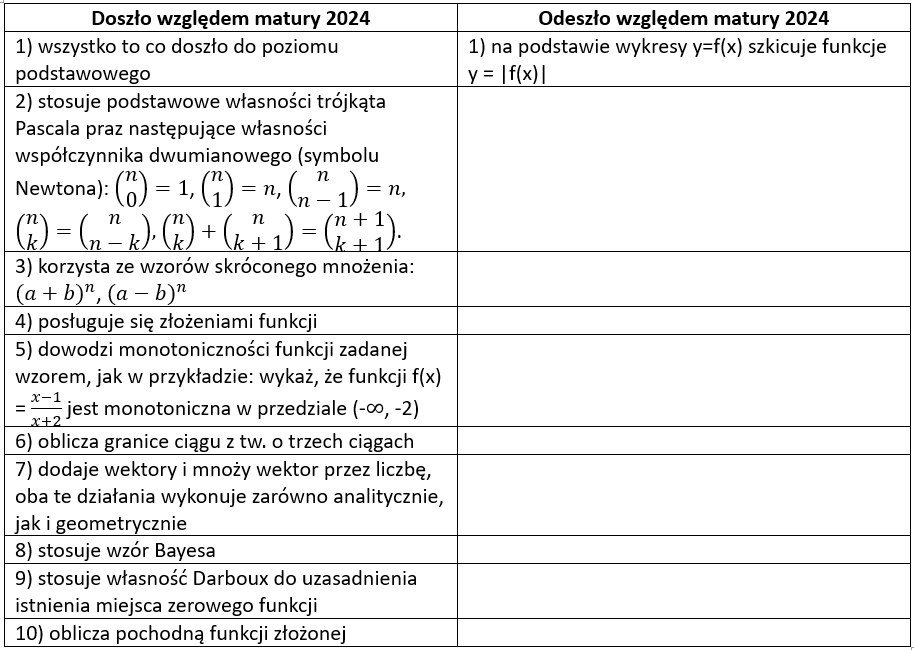
Zmiany względem podstawy programowej matury 2024 dla poziomu rozszerzonego przedstawia poniższa grafika:
Bibliografia do całego tekstu:
[1] matematyka.pdf
(cke.gov.pl)
[2] Informator_EM2023_matematyka_PP.pdf
(cke.gov.pl)
[3] Aneks_2023_2024_matematyka_EM_PP_F23.pdf
(cke.gov.pl)
[4] Informator_EM2023_matematyka_PR.pdf
(cke.gov.pl)
[5] Aneks_2023_2024_matematyka_EM_PR_F23.pdf
(cke.gov.pl)


